Scale Effect & Spatial Data Aggregation

Scale effects on vector data seem to be intuitive.  When you taking real earth and shrinking it down to fit on a page there will be details that will be lost or moved or changed.  Does your map scale allow for rivers, how about major creeks, does it show smaller tributaries?  The details that are not the focus are often eliminated the details that are the focus maybe included but require shifting of other features to get them to fit.

Resolution effects on raster data are also intuitive.  This is easiest demonstrated by a discussion of pixel.  The high the number of pixel for a photo the larger the picture can be made without looking blurry.  Raster data is contained in grids of cells.  At smaller cell size, 1m or 2m,  the more detail is available.  As the cell size gets to be larger (10m, 30m, 90m) the sample data is averaged in those cells.  The creates smoother data as the highs and lows are lost in the averaging.  And the imagery becomes more pixelated at finer resolution.

Modifiable Area Unit Problem (MAUP) exists for aggregation and zonation. Just because there are more area units does not mean the data is more specific and granular.  I can combine several areas to make larger areas and then put many many small areas into the mix.  I may end with more areas, but less detail than a lower number of evenly distributed area units.

Gerrymandering refers to odd shapes that can arise in political districts when the boundaries are manipulated for statistical properties.  Include this set of people and exclude those and we can raise or lower all kinds of statistics.  Determining the Polsby-Popper score results in a range 0-1.  The closer to 1 the more compact a polygon.  Polsby-Popper was calculated as 4*pie*area / perimeter^.  Below in red are the top 5 Congressional Districts in the Continental US that have lowest compact score, indicating the highest probability of gerrymandering.

Surfaces - Accuracy in DEMs

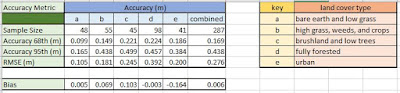
This week we examined vertical accuracy of DEMs.  We were provided with a raster file of high resolution bare earth DEM obtained through LIDAR and and excel file with field observations of ground elevation.  The field data contained 5 land cover types (a-e).  We utilized the Extract Multi Values to Points tool.  This tool grabs the elevation value of the pixel of the lidar raster directly beneath each sample point.  We added a field to the attribute table to convert feet to meters.  Accuracy was calculated for each land cover type and then the all the data combined.  We summarized the comparison in the table above.  The calculations in the table are the differences in meters from the DEM to the reference field data at 68%, 95%, RMSE, and Bias.

RMSE

• difference between DEM and reference for each point
• Square the difference for each point
• Average the squared differences (Sum the square difference/count of points)
• Square root of the average 

Bias as ME - is the average of the errors

Interpolation

 This week we carried out different surface interpolation techniques.  To the right you will see:

1)IDW:  Inverse Distance Weighting.  This was performed with IDW tool.  Generally the process takes the known sample points and infers values at other points.  This is accomplished by taking the known values and assuming areas in proximity of this will have similar results.

 2)Spline Interpolation Regularized: This method utilizes minimum curvature to fit boundary divisions through and around sample values.  I imagine laying out a piece of yard around the data values to form the boundaries for classifications.

3) Spline Interpolation Tension:  This method again utilizes minimum curvature to fit boundary divisions through the sample values.  Tension setting causes the barrier lines to be a bit more stiff, displaying as less fluid.

TINs and Dems

This week we moved from data quality to started looking at surface information.  We created 3d visualizations of elevation models, and examined TINs and DEMs.   

TIN, Triangular Irregular Network, is a vector display of triangles formed between elevation points the sides or edges of the triangles cover the study area without overlap or gaps to interpolate changes in elevation over distance to provide estimates of slope. Displayed above is a TIN.  The triangular network is visible with graduated color of slope and contour lines with darker index contours.

DEM, Digital Elevation Model, utilizes raster data stored in the raster cells.  The cell data is processed utilizing a model like nearest neighbor, 8 cell window, or other to provide elevation data.

This week we discovered how complicated it can be to calculate completeness of road networks.  First to calculate completeness is a comparison to another source of data (so depends on how complete/correct that information is, more about this in a minute).  We read a few articles on methods and data sets of comparing road centerlines.  Then in lab we compared a data set from Jackson County, Oregon to the 2000 TIGER Road data.  Seo, 2009, reports 2000 TIGER data was so poor that it required an extensive overhaul to be able to better meet the needs of the 2010 Census (Seo, 2009).  Going into this lab with the knowledge of the 2000 TIGER data I had expectations that the County Centerline data would be far more complete.  The choropleth above shows 297 grid cells, of those 162 show Local info to have less road kilometers than Tiger data, 134 cells show the local data to have more kilometers and 1 cell had no road kilometers in either data set.  The cells in green show where more kilometer or roads were found in the TIGER data than in the local County.  The darker the color the higher the percentage of  difference.  This depiction does not question if more kilometers of roads is a good method of calculating more complete data. 


Reference:

Seo, S., & Ohara, C. G. (2009). Quality assessment of linear data. International Journal of Geographical Information Science, 23(12), 1503–1525. doi: 10.1080/13658810802231456

Data Quality-Standards

This week in class we examined the accuracy of two road networks, Street Map and City of Albuquerque.  We calculated accuracy with procedures provided by the National Standard for Spatial Data Accuracy (NSSDA).  We selected 20 street intersection locations and marked the location of the intersection provided in the Street Map data as well as the same intersection location for the City data.  We referenced each of these data sets with ortho-rectified imagery.  The test points are shown above in green for the city data, red for the street map and blue (slightly larger symbol) for the reference.  Finding appropriate test points was more challenging that I initially thought.  20 minimum points, with a minimum of 20% in each quadrant with minimum separation between points of 10% of the diagonal of the study area.

Accuracy Statistics were calculated seperately for City data and Street Map each utilizing the Ortho points as the reference.  The XY data of each point was obtained in ArcPro.  Those points were exported to Excel.  The calculations included differences for X & Y coordinates, each difference squared, and then the sum of X & Y.  Those sets were summarized as Sum, Average, RMSE, and NSSDA.

Formal accuracy statements as per the NSSDA guidelines are:

Horizontal positional accuracy for Street Map:  Tested 70,116.2 Feet horizontal accuracy at 95% confidence level.

Horizontal positional accuracy for City of Albuquerque: Tested 605.8 Feet horizontal accuracy at 95% confidence level.

 
The accuracy position at 95% confidence is quite different:  City data at 605.8 feet; Street Map at 70,116.2 feet.  The importance of knowing the source of your data as well as its accuracy became abundantly apparent! 

Calculating Metrics for Spatial Data Quality

Horizontal Precision @68% 5.65meters

Vertical Precision @68% = 5.71meters

Horizontal Accuracy from the average point is 5.82 meters

Vertical Accuracy from the average point is 5.96 meters

Week one of Special Topics:  Learning Outcomes 1)understand the difference between precision and accuracy 2) calculate vertical and horizontal position accuracy and precision 3) calculate root-mean-square error (RMSE) and cumulative distribution function (CDF).

What is the difference between Accuracy and Precision?  Our text reports "Positional accuracy measures how close a representation of an object is to the true value." (Bolstad, 2017, p. 264).  And "Precision refers to the consistency of a measurement method." (Bostad, 2017, p. 264).  Another source describes it as "The accuracy of a measurement means getting a value that is close to the actual answer. Precision, on the other hand, refers to the reproducibility of this result that is you get the same result every time you try." (Nedha, 2015, para 1).  So precision is the repeatability of the results, and accuracy is how close to the referenced point (actual location).  

Precision for this lab was measured by calculating the % of precision desired (common is 68%) of the total sample points.  Sorting sample points from lowest to highest values and utilizing the measurements of the nth(68% of 50 sample is 34) sample.

Accuracy for this lab was measured by calculating the average of all sample points and comparing it to the referenced/actual point.

Reference:

Bolstad, P. (2017). Gis fundamentals: a first text on geographic information systems. Acton, MA: XanEdu.

Nedha. (2015, July 13). Difference Between Accuracy and Precision. Retrieved from https://www.differencebetween.com/difference-between-accuracy-and-vs-precision/

Final Project: Collin County Residential Property Value

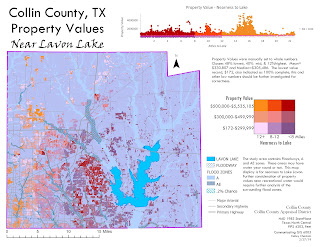
My final project for Communicating GIS 6005 was to examine limited variables correlation to single family property values in Collin County, Texas.  The variables considered were number of bedrooms, number of bathrooms, age of property and nearness to Lavon Lake.  Shapefiles for Lavon Lake boundary, Collin County boundary, roads, and floodplain boundary were obtained from Collin County.  Parcel data was obtained from Collin County Appraisal District.  The above infographic contains scatter plots for property value on the x axis and number of bathrooms (top) and number of bedrooms (bottom).  The age of the properties are displayed on purple with a black to white color ramp displaying oldest to newest properties.  The main display is of assessed property values shown on a color ramp from dark blue to bright yellow (low-high).  The main display also includes the floodplain for the area.  Finally in the main display, low in the hierarchy, are primary highways, secondary highways and major arterial roads.  Parcel data was limited to single family residential that were 100% complete and contained information on bathrooms, bedrooms and assessed property value.  Data should be further examined as the property values range from 172 to over $5.5 million.  Those properties of  very low values should be examined for error.

My second infographic includes a scatter plot and bivariate choropleth.  The scatter plot displays distance to lake on the x axis and property values on the y axis.  The bivariate choropleth displays property value in a 3 class manual display (< $300,000 = 48.0%, $300,000-$500,00 = 40.0% and above $500,000 11.8%) and nearness to Lavon Lake in a 3 class quantile class (rounded to whole numbers:  <8 miles = 36.68%, 8-12 miles = 31.5%, more than 12 miles = 31.82%).  The two variable legend classes from lower left as furthest from the lake (more than 12 miles and lowest property values at under $300,000.  to the highest lass upper right with nearest to the lake (within 8 miles) and property values over $500,000.  This display would indicate there is not a significant correlation between the two variables.  This may be due to the floodplain in the area containing floodways that may contain year round navigable waters, allowing access to recreational waters in areas other than the lake.

Module 6: Proportional Symbol and Bi-variate Choropleth

This week we learned about proportional symbol mapping and bi-variate choropleth (above).

Proportional symbol mapping is a quantitative map that varies the representation of a  feature, and the size, shape, and color vary with the particular variable. This type of map is very appropriate to map data counts.
Our first assignment was to utilize a proportional symbol map to represent the population size of cities in India.  First we were asked to determine the appropriate variables for a custom conic projection for the area.  I utilized a central meridian of 80E and parallels of 30.8N and 12.0N. The symbol properties for the proportional symbol were set with consideration of the background colors and visibility.  Finally a custom legend was created to show the range of symbols utilizing Flannery Appearance Compensation to accentuate the differences in the larger symbols.

Next we moved on to divergent proportional symbology to display jobs gained or lost by state in a time frame of December 2007 and July 2015.  This map creation had many challenges.  First the use of negative numbers does not work for this process.  The original shape file was divided into two shape files utilizing Select by Attribute SQL for <0 and >0.  In the file with the data <0, a new field was created, the field calculator was utilized to obtain the absolute value of those numbers (essentially making them positive).  Due to technical difficulties with loading this data (load times were extreme for even the smallest changes), and the two layers (gains and losses) being set to the same minimum size, line width, and no maximum created different size reference I tried to make the map as completely basic as possible. I am not satisfied with this map, but in the time frame and technical issues this is it.

Update:  Due to the technical issues with ArcPro with proportional symbol for raw count data that I encountered for the above map, I chose to change the symbolization for the raw count data to a dot density map.  More confident in the display of the data in this format.

Finally, we were asked to create a bi-variate choropleth map displaying two variables (% obesity and % physical inactivity)  Bi-variate choropleth maps display two variables (sometimes three = Tri- or Multi-variate) on the same map.  Variables for choropleth maps should be normalized.  These were in the form of %.  Each variable was classed into 3 class quantile classification in order to obtain the break values for the classes.  From the attribute table use of SQL to obtain the records for these classifications were then classed in new fields.  The completion of a column for each variable were then combined using concatenate to a third/final field.  The map was symbolized

with unique values from this final field.  Adjustments were performed to those unique colors by color ramp, complementary color wheel and filling in changes based on Hue (top left and bottom right are complementary - opposite on the color wheel, top right lies between on color wheel) , Saturation (very low or 0 in the bottom left and gradually increase to top right) and Value (lowest in the top right and lowest in the bottom left).  Here is a close up of the legend.  Map appears at top of this post.

Module 5: Analytics

This week we downloaded 2018 County Health Rankings National Data from http://www.countyhealthrankings.org/explore-health-rankings/rankings-data-documentation 
After downloading the data we were to review and choose two variables that could be related and create an info-graphic from the variables. "The County Health Rankings are based on counties and county equivalents.  The data is a variety of national and state sources that are standardized and combined using scientifically-informed weights."(County Health Rankings & Roadmaps, 2019).

The objective of this lab assignment is to practice the use of a number of different data visualization techniques, including bar charts and scatter plots, as well as the design of communication materials that combine maps and other graphics. We were to select appropriate chart types for our chosen data.  We then created charts for data visualization, including scatter plots, bar charts, and a pie chart.  Finally, we were to combine maps, charts, and text into a single data visualization product (above). 

I chose "% uninsured" and "% frequent mental distress".  I was unable to determine how "% frequent mental distress" was specifically determined, but feel the relationship to Mental Illness would be close.  My hypothesis was that the states with higher mental distress would also have higher uninsured rates.  The correlation being that those with mental illness not able to obtain treatment due to no insurance would lead to higher mental distress incidents.  The scatter plot of the two variables shows some correlation but not as strong as I had suspected.  The bar charts show the high and low states for the variable as well as the national, Florida and Alabama (my specific area).  The area chart illustrates how few of the population are not insured.  I also included a pie chart as well as a simple graphic to show 1 out of 25.

Reference:
County Health Rankings & Roadmaps. (2019). Retrieved from: http://www.countyhealthrankings.org/explore-health-rankings/our-methods [Accessed 8 Feb. 2019].

Module 4: Color and Choropleth

This week's project was to pick one state from a list provided and extract the state information and map the population change from 2010 to 2014.  I picked Colorado.  Colorado has 2 UTM zones and 3 StatePlane, so these were eliminated as projection choices.  I did not locate a projection specific for the State of Colorado.  I chose to use NAD 1983 (2011) Contiguous USA Albers.  A custom Albers projection adjusted with central meridian and standard parallel would have been better, but I couldn’t figure out how to change them.  The formula I utilized to normalize data to percent of change in population is: (Population 2014-Population 2010)/Population 2010*100.  I used an 8 class manually assigned classification.  I after looking at the natural breaks for a 5 class I decided to take the natural breaks and round them to more user friendly intervals keeping significant breaks for both growth and loss of population.  I also added a critical class for the 0 marker.  I utilized a divergent color scheme to help symbolize those that population increased/decreased.  Darkening greens to indicate increased growth and progressively darker grays for loss of population.

Module 3 - Terrain Visualization

This week we studied terrain visualization.  We considered contour lines, DEM, hillshade single and multiple light source, and color tinting.  The above map utilized an elevation raster provided for Yellowstone National park and a land cover raster.  The elevation raster was processed with a single light source hillshade tool from the Raster function in the Raster group of the Analysis tab in ArcPro.  The land cover raster categories were generalized into fewer groups and appropriate colors were chosen for each group.  The land cover layer is displayed at 45% transparency to allow the hillshade texture to show through.  Legibility of the map text and message are clear.  Visual Contrast is sufficient to distinguish categories but not abrasive.  Figure Ground is clear between the boundaries of the land cover of Yellowstone park and the grey tones of the hillshade outside of the park.  Hierarchy is demonstrated in text size and element location.  Title is largest text and subtitle is smaller and more ornate.  The north arrow is placed within a non-focus part of the map frame.  The projections and class are in larger font and positioned above author name and date.  Balance was addressed with a centered map frame and main title, large legend is balanced with other map elements.

Module 2 - Coordinate Systems

This week in Communicating GIS we learned about Coordinates systems, Scale and Projections.  For the map above we were tasked with selecting one US State other than Florida and creating a general reference map layout for that area of interest.  The layout should be in a coordinate system appropriate for the state.  Although State Plane and UTM projections are quite common in the US, not all states fit in a single zone of said projections.  Texas has 5 State Plane zones and 3 UTM zones.  Projections for UTM and State Plane are zone specific and as such neither of these would be appropriate for the state of Texas.  Fortunately there are several projections that are appropriate for the entire state.  I chose to use NAD 1983 (2011) Texas Centric Map System.  This projections is a Lambert Conic conformal map.  The central meridian is at -100.  The standard parallels are at 27.5 and 35.0.  This projections is specific for the state of Texas and conformal, retains shape, making it an appropriate projection for a general reference map for Texas.